PG/PPO/DPO/GRPO/MDPO 公式推导

<think> 这篇博客的主要目的是整理强化学习中几个XPO的优化目标，包括比较经典的PPO、DPO，KIMI1.5中的MDPO以及DeepseekMath(R1)的GRPO。

Policy Gradient

首先从策略梯度(Policy Gradient)说起，广义的强化学习优化目标如下
$$\arg \underset{{\pi }_{\theta }}{max}J({\pi }_{\theta })={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )]=\sum _{\tau }R(\tau )P(\tau |{\pi }_{\theta })$$
简单来说就是如果当前轨迹$\tau$得到的奖励$R(\tau )$越大，那就增大采样$\tau$的概率。其梯度如下

对于LLM场景，${\pi }_{\theta }$指的就是模型本身，$\tau$则是它生成的一个句子。我们可以采样很多个句子$\tau$来估计期望(蒙特卡洛采样)

$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& =\sum _{\tau }R(\tau )\mathrm{\nabla }P(\tau |{\pi }_{\theta })\\ & =\sum _{\tau }R(\tau )P(\tau |{\pi }_{\theta })\frac{\mathrm{\nabla }P(\tau |{\pi }_{\theta })}{P(\tau |{\pi }_{\theta })}\\ & =\sum _{\tau }R(\tau )P(\tau |{\pi }_{\theta })\mathrm{\nabla }\log P(\tau |{\pi }_{\theta })\\ & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )\mathrm{\nabla }\log P(\tau |{\pi }_{\theta })]\end{array}$$

我们还可以对$P(\tau |{\pi }_{\theta })$做一定简化，因为$\tau =(s_0,a_0,s_1,a_1,...,s_t)$，所以
$$P(\tau |{\pi }_{\theta })={\rho }_0(s_0)\prod _{t=0}^{T-1}P(s_{t+1}|s_t,a_t){\pi }_{\theta }(a_t|s_t)$$
而初始状态$s_0$和状态转移概率$P(s_{t+1}|s_t,a_t)$都和策略${\pi }_{\theta }$无关，所以
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )\mathrm{\nabla }\log P(\tau |{\pi }_{\theta })]\\ & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )\mathrm{\nabla }[\log {\rho }_0(s_0)+\sum _{t=0}^{T-1}\log P(s_{t+1}|s_t,a_t)+\sum _{t=0}^{T-1}\log P(a_t|s_t)]]\\ & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )\sum _{t=0}^{T-1}\mathrm{\nabla }\log P(a_t|s_t)]\end{array}$$
这个就是策略梯度的最终形态了，之后我们可以看到PPO/GRPO都可以用从这个式子出发

PPO

PPO首先改造的是$R(\tau )$，它将其分割到每一个时间步$R(s_t,a_t)$中，字面意思就是在$s_t$状态执行$a_t$的回报，相比于t时刻的奖励$r_t$，这个回报如果能考虑未来的奖励情况就更好了，比如$R^{\prime }(s_t,a_t)=\sum _{k=t}^{T-1}{\gamma }^{k-t}\ast r_k$。

刚刚提到的$R^{\prime }(s_t,a_t)=\sum _{k=t}^{T-1}{\gamma }^{k-t}\ast r_k$虽然考虑了实际的未来奖励值，但是每一个r都是随机变量，这会导致$R(t)$的方差很大。所以有没有可能用一个函数去估计$R^{\prime }(s_t,a_t)$呢？

于是这里引入了critic model和$V(t)$，t时刻的平均(不管执行什么动作)回报叫做$V(t)$，critic model的工作是估计$V(t)$，而此时$R(s_t,a_t)=r_t+\gamma \ast V(t+1)-V(t)$，这个形式其实就是TD Error，直观上理解，$V(t)$是t时刻的平均回报，$r_t+\gamma \ast V(t+1)$是在t时刻执行动作$a_t$得到的奖励加上t+1时刻的折扣回报，也就是考虑了当前时间步的动作的总回报，那么$R(s_t,a_t)$则是当前t时刻，执行$a_t$动作得到的回报比平均回报多的部分。换而言之，$R(s_t,a_t)$也可以叫做优势。既然$V(t)$和$V(t+1)$都是模型(critic model)估计的，那怎么设计它的损失函数呢？

critic model的损失函数其实就是$R(s_t,a_t)$本身，这里我们可以参考最早的$R^{\prime }(s_t,a_t)=\sum _{k=t}^{T-1}{\gamma }^{k-t}\ast r_k$，它满足$R^{\prime }(s_t,a_t)=r_t+\gamma R^{\prime }(s_{t+1},a_{t+1})$，我们自然也希望$V(t)$也具备$R^{\prime }(s_t,a_t)$一样的性质。另外用一个模型去估计V，带来的方差会小一点(毕竟专门拿了一个模型来学V，它见过其他的轨迹$\tau$，学习到的value方差也会小一点)

有人可能会觉得《critic model的损失函数其实就是$R(s_t,a_t)$本身》，那优势$R(s_t,a_t)$被优化到0了，我的策略模型岂不是没法更新了？事实上，如果$R(s_t,a_t)$如果是0，说明此时做什么动作都不会影响到最后的奖励期望，那这个时候已经是最优策略${\pi }^{\ast }$了，自然也没有必要做策略提升

此时的$R(s_t,a_t)$强依赖于critic model估计的$V(t)$，但是$V(t)$更新时只考虑到了当前轨迹当前动作$a_t$所带来的$r_t$，偏差比较大。(这里解释偏差比较抽象，我的理解是学出来的$V(t)$虽然满足$r_t+\gamma \ast V(t+1)=V(t)$这个相对关系约束，但是因为有t个未知数，t-1个方程，学出来的V不是确切解，可能存在偏差)

所以PPO最终采用的是GAE，即权衡了偏差和方差的最终版本$\mathrm{\Phi }(s_t,a_t)$。它是$R(s_t,a_t)$和$R^{\prime }(s_t,a_t)$之间的trade off，通过一个$\lambda$超参调整之间的比例。
$$\begin{array}{rl}{\delta }_t& =r_t+\gamma V(t+1)-V(t)\\ {\mathrm{\Phi }}_{s_t,a_t}& =\sum _{k=0}^{\mathrm{\infty }}(\gamma \lambda {)}^k{\delta }_{t+k}\end{array}$$
当$\lambda =0$，$\mathrm{\Phi }(t)$退化成$R(s_t,a_t)$；当$\lambda =1$，$\mathrm{\Phi }(t)$退化成$R^{\prime }(s_t,a_t)-V(t)$

$R^{\prime }(s_t,a_t)-V(t)$是$R^{\prime }(s_t,a_t)$的baselined版本，这里同样学了一个V(t)，就不展开了

使用$\mathrm{\Phi }(s_t,a_t)$时，critic model的损失就得换成$\mathrm{\Phi }(s_t,a_t)+V(t)-V(t)=\mathrm{\Phi }(s_t,a_t)$，把广义优势当成损失

说完了$R(t)$，这个时候回过头看$\mathrm{\nabla }J({\pi }_{\theta })$，他现在可以表示为
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[\sum _{t=0}^{T-1}\mathrm{\Phi }(t)\mathrm{\nabla }\log P(a_t|s_t)]\end{array}$$
接下来再带入${\pi }_{\theta }$经过on policy到off policy的转变(之前博客提到了)，我们可以得到
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{old}}[\sum _{t=0}^{T-1}\mathrm{\Phi }(t)\frac{\mathrm{\nabla }{\pi }_{\theta }(a_t|s_t)}{{\pi }_{old}(a_t|s_t)}]\end{array}$$
那么优化目标也就是
$$\begin{array}{rl}J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{old}}[\sum _{t=0}^{T-1}\mathrm{\Phi }(t)\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{old}(a_t|s_t)}]\end{array}$$
这里${\pi }_{\theta }$是要更新的model，而${\pi }_{old}$是拿来采样$\tau$的model。off policy希望这两个model分布不要相差太大，所以我们可以再加一项KL散度约束(这里是反向的KL散度，可能之后再出一篇说)
$$\begin{array}{rl}J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{old}}[\sum _{t=0}^{T-1}\mathrm{\Phi }(t)\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{old}(a_t|s_t)}]-\beta KL[{\pi }_{\theta }(\cdot |s_t)||{\pi }_{old}(\cdot |s_t)]\end{array}$$
以上就是PPO的Policy优化目标啦，这里省略了对优势的裁剪操作(训练critic model的时候也可以对V做裁剪)。

KL那一项如果拿出来，作为$J({\pi }_{\theta })$的约束条件，则是TRPO的做法

另外这里还省略了奖励模型的训练，$r_t$的设置，可以参考上一篇博客

关于奖励模型的优化目标，请见下一章DPO

DPO

PPO首先要训一个奖励模型，再逐步更新actor/critic model，显得太繁琐了。DPO的想法就是绕过奖励模型。

PPO的训练目标还可以写成以下这种广义的形式
$$\begin{array}{rl}J({\pi }_{\theta })& =\underset{\pi }{max}{\mathbb{E}}_{x\sim D,y\sim \pi }[r(x,y)]-\beta {\mathbb{D}}_{\text{KL}}[{\pi }_{\theta }(y|x)||{\pi }_{ref}(y|x)]\end{array}$$
第二项还是KL散度，而第一项在最大化采样句子$\tau =x+y$的奖励期望，PPO在这里的做法是训了一个奖励模型来拟合$r$函数，同时为了和LLM next token prediction的token级别action对齐，把reward拆解成了多个时间步，并训练了一个critic model预测当前时间步的未来平均回报$V$。

DPO则表示不急，还想继续推导一下$J({\pi }_{\theta })$，于是有
$$\begin{array}{rl}J({\pi }_{\theta })& =\underset{\pi }{max}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[r(x,y)]-\beta {\mathbb{D}}_{\text{KL}}[{\pi }_{\theta }(y|x)||{\pi }_{ref}(y|x)]\\ & =\underset{\pi }{max}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[r(x,y)-\beta \log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)}]\\ & =\underset{\pi }{min}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)}-\frac{1}{\beta }r(x,y)]\\ & =\underset{\pi }{min}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)\cdot \exp [\frac{1}{\beta }r(x,y)]}]\\ & =\underset{\pi }{min}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[\log \frac{{\pi }_{\theta }(y|x)}{\frac{1}{Z(x)}{\pi }_{ref}(y|x)\cdot \exp [\frac{1}{\beta }r(x,y)]}-logZ(x)]\end{array}$$
其中$Z(x)=\sum _y{\pi }_{ref}(y|x)\exp [\frac{1}{\beta }r(x,y)]$，构造Z的原因是，DPO想把第一项写成KL散度的形式，那么分母也应该满足概率分布的条件，于是Z(x)就负责把它归一化到[0,1]

现在我们得到了一个新的概率分布${\pi }^{\ast }=\frac{1}{Z(x)}{\pi }_{ref}(y|x)\cdot \exp [\frac{1}{\beta }r(x,y)]$，$J({\pi }_{\theta })$的目标是拉近${\pi }_{\theta }$和它的距离。
$$\begin{array}{rl}J({\pi }_{\theta })& =\underset{\pi }{min}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[\log \frac{{\pi }_{\theta }(y|x)}{\frac{1}{Z(x)}{\pi }_{ref}(y|x)\cdot \exp [\frac{1}{\beta }r(x,y)]}-logZ(x)]\\ & =\underset{\pi }{min}{\mathbb{E}}_{x\sim D,y\sim {\pi }_{\theta }}[\text{KL}[{\pi }_{\theta }(x)||{\pi }^{\ast }(y|x)]-logZ(x)]\end{array}$$
另外$\log Z$只和${\pi }_{ref}$有关，所以只需要优化第一项即可。这个时候我们可以写出${\pi }_{\theta }$的最优解！就是我们刚刚构造的${\pi }^{\ast }$！(两个概率分布相等时KL散度为0)

这时候我们可以得到给定$r$可以训练得到的最优${\pi }_{\theta }^{\ast }$
$${\pi }_{\theta }=\frac{1}{Z(x)}{\pi }_{ref}(y|x)\cdot \exp [\frac{1}{\beta }r(x,y)]$$
变换一下可以得到$r$和${\pi }_{\theta }^{\ast }$之间的关系，那么下一步是不是意味着我们在训练奖励模型的时候用等式右边替换，就可以把优化对象从奖励模型$r$切换到${\pi }_{\theta }^{\ast }$了？
$$r(x,y)=\beta \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{ref}(y|x)}+\beta \log Z(x)$$
接下来回顾一下奖励模型的优化目标是什么，OpenAI的RLHF-PPO的做法和这里一样(应该是DPO和PPO一样)
$$J_r(r,D)=max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log P(y_w>y_l|x)]$$
这里用Bradley-Terry刻画了概率$P(y_w>y_l|x)=\frac{e^{{\lambda }_1}}{e^{{\lambda }_1}+e^{{\lambda }_2}}$，其中${\lambda }_1,{\lambda }_2$是$y_w,y_l$的强度参数，我们可以用奖励值代替，那么优化目标就变成
$$\begin{array}{rl}{J}_r(r,D)& =max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log P(y_w>y_l|x)]\\ & =max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log \frac{e^{r(x,y_w)}}{e^{r(x,y_w)}+e^{r(x,y_l)}}]\\ & =max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log \frac{1}{1+e^{-[r(x,y_w)-r(x,y_l)]}}]\\ & =max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log \sigma [r(x,y_w)-r(x,y_l)]\end{array}$$
其中$\sigma$是sigmoid函数，这个形式和InstructGPT就一样了。理解也很直接：好的句子的reward比坏的句子的reward高就行。

这个优化目标只要求两者之间的相对关系，所以DPO训练的时候有可能出现两个句子采样概率都变低了，但是因为坏句子采样概率降低的更快，所以.......

OK，推导这一步，我们只需要把刚刚求的$r$带入到这个优化目标中，就可以得到DPO最终的优化目标了
$$\begin{array}{rl}{J}_r(r,D)& =max{\mathbb{E}}_{(x,y_w,y_l)\sim D}[\log \sigma [\beta \log \frac{{\pi }_{\theta }^{\ast }(y_w|x)}{{\pi }_{ref}(y_w|x)}-\beta \log \frac{{\pi }_{\theta }^{\ast }(y_l|x)}{{\pi }_{ref}(y_l|x)}]\end{array}$$
注意这里的几个$\pi$分布都是句子级别的，所以在代码实现时，会把所有token的logprobs之差都加起来。

GRPO

DeepSeek R1的Iterative GRPO最近关注度非常高，也有很多开源项目在follow。但是GRPO本身复现也有些争议，所以这里只简单介绍一下DeepseekMath里提到的公式。

说回最早的策略梯度, $R(\tau )$的设计百花争鸣，有多次采样未来奖励的形式、也有用critic model估计优势的形式、还有两者结合的GAE，有时还需要加上裁剪、KL散度，这些设计无疑都比较繁琐。(这些设计，包括前段时间的MCTS，都是过程奖励模型)
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )\sum _{t=0}^{T-1}\mathrm{\nabla }\log P(a_t|s_t)]\end{array}$$
GRPO则探索了另一个方向，首先设计容易验证的问题和答案，使用ruled-based的奖励模型(结果奖励模型)。

举个例子，我希望模型输出的内容包括思维链和最终答案，思维链被tag \<think> \<\think>包裹，如果模型生成的句子有这两个tag，就给一定的奖励。

现在奖励来源搞定了，但是怎么体现“优势”呢(之前讨论PPO的优势时我们还提到一个baseline的版本，一个相对奖励会更好优化些)，GRPO的做法是采样多条路径$o=(o_1,...,o_g)$为一组，每组计算归一化后的奖励(假设一组采样g次)
$$A_{i,t}=r_i=\frac{r_i-mean(r)}{std(r)},r=(r_1,r_2,...r_g)$$
那么优化的目标就是
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& ={\mathbb{E}}_{(o_1,o_2,...,o_g\sim {\pi }_{\theta })}[\sum _{t=0}^{T-1}{A}_{i,t}\mathrm{\nabla }\log {\pi }_{\theta }(a_t|s_t)]\\ & =\frac{1}{G}\sum _{i=1}^G\frac{1}{T}\sum _{t=0}^{T-1}{A}_{i,t}\mathrm{\nabla }\log {\pi }_{\theta }(a_t|s_t)\end{array}$$

细心的小伙伴会发现这里多了一个$1/T$，这其实等效于$A_{i,t}$的值除以当前这个句子的长度，GRPO为什么要这么做呢？因为我们设计$A_{i,t}$的时候一个句子每个token(t)位置的奖励都是整个句子的奖励$r_i$,所以这里可以认为是把整体奖励平均分给每个token。

我们再加上PPO里也用上的重要性采样，以及KL散度，就可以得到论文里的公式了
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& =\frac{1}{G}\sum _{i=1}^G\frac{1}{T}\sum _{t=0}^{T-1}\{min[\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{old}(o_{i,t}|q,o_{i,<t})}{A}_{i,t},\text{clip}(\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{old}(o_{i,t}|q,o_{i,<t})},1-ϵ,1+ϵ)A_{i,t}]\\ & -\beta {\mathbb{D}}_{KL}[{\pi }_{\theta }||{\pi }_{ref}]\}\end{array}$$
trl也实现了GRPOTrainer，但是实现和上面的式子不太一样，比如上式是off policy，而实现时用的是on policy，于是可以去掉clip，因为比值是1(但是这里为什么不直接用策略梯度的$\log {\pi }_{\theta }$还没有定论)

对源码感兴趣的同学可以参考GRPO Trainer

另外，R1用的实际上是Iterative GRPO，${\pi }_{ref}$也会逐步更新，这里就不展开了

再补充一点，KL散度的计算采用了Schulman估计，之后可能会展开讲，估计的好处是方差比较小(尽管直接算$\log \frac{q}{p}$是无偏的)

MDPO-K1.5

MDPO是KIMI k1.5用到的RL方式，来自Mirror Descent Policy Optimization。它其实和GRPO有点相似，但是理论基础更多一点。

首先K1.5也使用ruled-based的奖励模型(结果奖励模型)，简化了r的设计。

其次我们在DPO推导出了$r$函数和最优策略${\pi }_{\theta }^{\ast }$的关系
$$r(x,y)=\beta \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{ref}(y|x)}+\beta \log Z(x)$$
目前$r$已知，$Z(x)=\sum _y{\pi }_{ref}(y|x)\exp [\frac{1}{\beta }r(x,y)]$；我们构造一个代理损失来优化${\pi }_{\theta }$
$$L(\theta )=(r(x,y)-\beta \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{ref}(y|x)}-\beta \log Z(x){)}^2$$
我们稍微规范一下符号(与论文中对齐)，x为quesiton，y为ref model采样的response，$y^{\ast }$为标准答案，D为数据集，KL散度因子用$\beta \to \tau$。我们可以得到
$$L(\theta )={\mathbb{E}}_{(x,y^{\ast })\sim D}[{\mathbb{E}}_{(y,z)\sim {\pi }_{{\theta }_i}}[(r(x,y,y^{\ast })-\tau \log Z(x)-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^2]]$$

注意${\pi }_{ref}$换成了${\pi }_{{\theta }_i}$，这是因为这里的算法也是Iterative的，但是我们先只看一次迭代

另外注意这里采样句子的是${\pi }_{{\theta }_i}$(ref model)，而不是${\pi }_{\theta }$或之前提到的重要性采样模型${\pi }_{old}$，我的理解是它这里从ref model采样句子是为了估计$Z(x)$。同时也是因为这个原因，ref model也需要迭代式的更新，来保证采样的句子和我们最后要的${\pi }_{\theta }$生成的句子分布接近

继续考虑Z的估计，假设从${\pi }_{{\theta }_i}$采样了$(y_1,z_1),(y_2,z_2),...,(y_k,z_k)$ ，那么$Z(x)\approx \frac{1}{k}\sum _{i=1}^k\exp [r(x,y_i,y^{\ast })/\tau ]$。($z_i$指的是思维链，我们可以先把它和$y_i$一起考虑)

接下来重点来了，实际应用时$\tau \log Z(x)$可以直接用$\overline{r}=mean(r(x,y_1,y\ast ),..,r(x,y_k,y^{\ast }))$来表示。这是因为采样次数足够多时，
$$\begin{array}{rl}\tau \log Z(x)& \approx \tau \log \frac{1}{k}\sum _{i=1}^k\exp [r(x,y_i,y^{\ast })/\tau ]\\ & \approx \tau \log \frac{1}{k}\cdot k\cdot \exp [\overline{r}(x,y_i,y^{\ast })/\tau ]\\ & \approx \overline{r}(x,y_i,y^{\ast })\end{array}$$
OK，最后我们得到了
$$L(\theta )={\mathbb{E}}_{(x,y^{\ast })\sim D}[{\mathbb{E}}_{(y,z)\sim {\pi }_{{\theta }_i}}[(r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^2]]$$
开始求梯度！(先忽略掉两个期望值)
$$\begin{array}{rl}\mathrm{\nabla }L(\theta )& =[(r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^2{]}^{\prime }\\ & =2\cdot (r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)})(r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^{\prime }\\ & =2\cdot (r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)})(-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^{\prime }\\ & =-2\tau \cdot (r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)})(\log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}{)}^{\prime }\\ & =-2\tau \cdot (r(x,y,y^{\ast })-\overline{r}-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)})\mathrm{\nabla }\log {\pi }_{\theta }^{\ast }(y|x)\\ & =-2\tau \cdot ({\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }^{\ast }(y|x)[r(x,y,y^{\ast })-\overline{r}]-\tau \log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)}\mathrm{\nabla }\log {\pi }_{\theta }^{\ast }(y|x))\\ & =-2\tau \cdot ({\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }^{\ast }(y|x)[r(x,y,y^{\ast })-\overline{r}]-\frac{\tau }{2}{\mathrm{\nabla }}_{\theta }{(\log \frac{{\pi }_{\theta }^{\ast }(y|x)}{{\pi }_{{\theta }_i}(y|x)})}^2)\\ & =\frac{-2\tau }{k}\sum _{i=1}^k\cdot ({\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }^{\ast }(y_i,z_i|x)[r(x,y_i,y^{\ast })-\overline{r}]-\frac{\tau }{2}{\mathrm{\nabla }}_{\theta }{(\log \frac{{\pi }_{\theta }^{\ast }(y_i,z_i|x)}{{\pi }_{{\theta }_i}(y_i,z_i|x)})}^2)\end{array}$$
最后一步考虑了${\mathbb{E}}_{(y,z)\sim {\pi }_{{\theta }_i}}$，另外把输出y拆解成了输出$y$和思维链$z$，可以看到这个式子和论文中的只差了常数项$-2\tau$，这应该是论文漏写了。

后记

至此PPO/DPO/GRPO/MDPO-K1.5所有的公式推导基本都放在这里了，还有一些重要性采样(上篇博客介绍了)，裁剪、Iterative的操作这里为了简洁就省略了。

回顾这几个算法的设计，可以看到从PRM到ORM的转变，从一个复杂的reward/critic model到ruled-based model，从policy-base和value-base结合的ppo到纯policy-base的grpo，整个强化学习的pipeline是不断在简化的。(又让我想起来经典的The bitter lesson)

KIMI1.5论文里介绍了PRM到ORM转变的原因：通过value去估计某个action的优势，可能会导致有些不那么错的action采样概率降低(比如$s_t$状态下，一个action a通向正确的结果，而另一个action b通向了差一点点就正确的结果，那么动作a会被鼓励而动作b会被抑制)，这降低了模型去trial and error的可能性，也就是所谓的“aha moment”。从这个角度看ORM可能会好一点，但是ORM奖励并不是token/action级别的，现在几个算法都是直接平均分摊，可能这个点还可以做一下？

不管怎么讲，这篇博客到这就该结束了。这几天追热点确实很过瘾，但也愈发觉得自己的渺小，只能写点文字聊以慰籍，留下一些痕迹。

博客又何尝不是一种思维链呢(突然想起来之前博客被人爬了，会不会有某个LLM记得JJJYmmm🤣)

</think>

附录

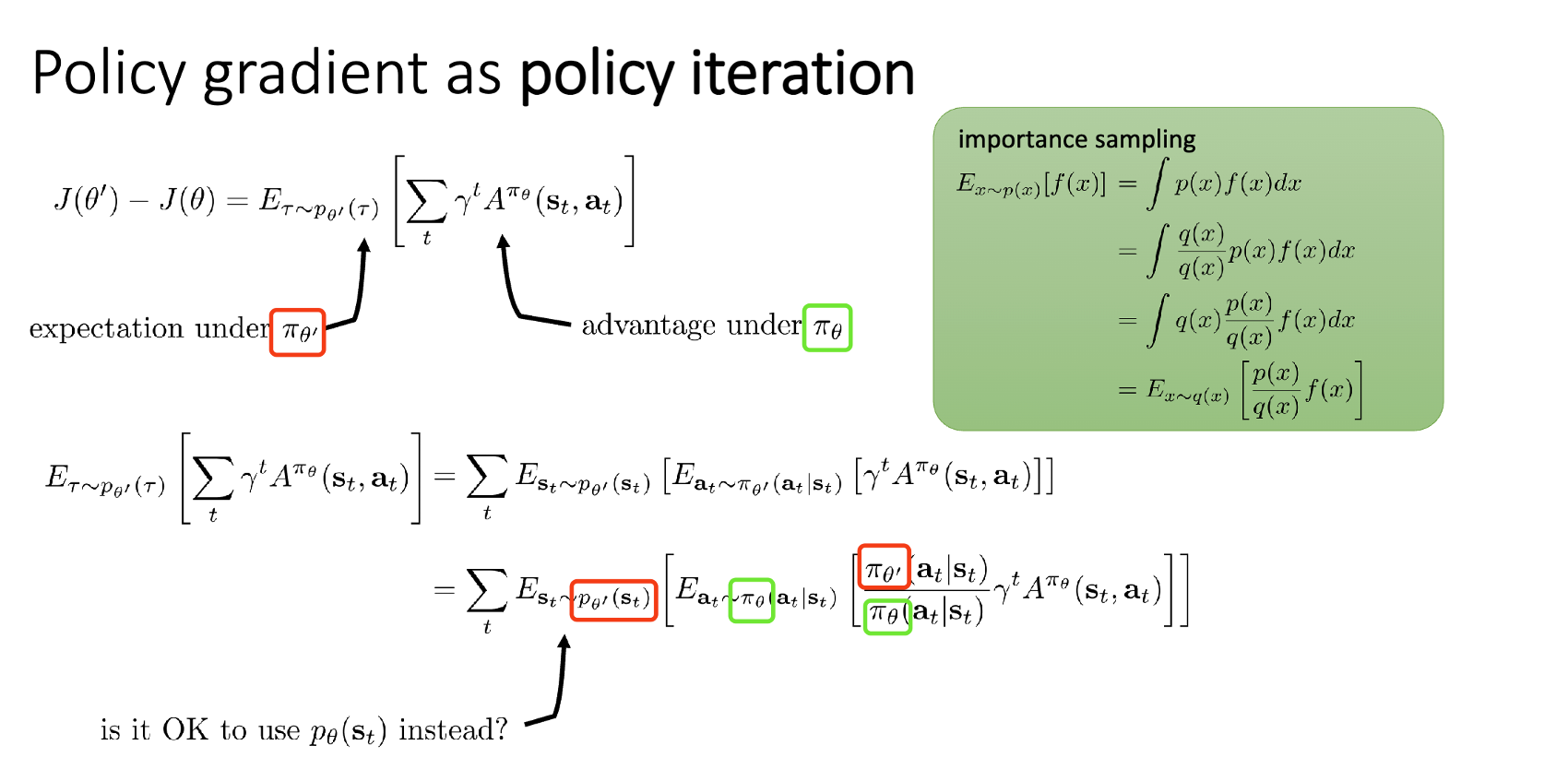
Qingbin大佬指出PPO的$\mathrm{\nabla }J({\pi }_{\theta })$可能不太严谨，但数值上相差不大(附上他提供的cs285 slides)
$$\begin{array}{rl}\mathrm{\nabla }J({\pi }_{\theta })& =J({\pi }_{\theta }^{\prime })-J({\pi }_{\theta })\\ & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }^{\prime }}[\sum _{t=0}^{T-1}\mathrm{\Phi }(t)\mathrm{\nabla }\log P(a_t|s_t)]\\ & ={\mathbb{E}}_{\tau \sim {\pi }_{\theta }^{\prime }}[\sum _{t=0}^{T-1}{\mathrm{\Phi }}^{{\pi }_{\theta }}(t)\mathrm{\nabla }\log {\pi }_{\theta }^{\prime }(a_t|s_t)]\end{array}$$